- Representando el atractor de Lorenz con C++20, Boost.Numeric.Odeint y Dlib
- Análisis dimensional con mp-units, regresiones no-lineales con Dlib.Optimization y visualización de datos con Matplot++
- Rectas de mejor ajuste por mínimos cuadrados (mp-units, Matplot++)
- Ceros de una función
- Comprobando la ley de Zipf
- Instalación de Matplot++ y mp-units con Mingw-w64
Como extensión natural del segundo artículo de esta serie, este post analiza la obtención de rectas de mejor ajuste mediante el método de mínimos cuadrados sirviéndose de las bibliotecas de análisis dimensional mp-units [1] y de representación de datos Matplot++ [2].
Consideremos un experimento de laboratorio en el que se mida la intensidad de campo magnético B en el centro de una espira de N = 3 vueltas y radio R = 60 mm cuando a través de ella circulan diversas intensidades de corriente eléctrica I. Teóricamente, debiera verificarse una relación lineal entre el campo B y la corriente I dada por:
B = μ0NI / (2R),
donde μ0 = 4π⨯10-7 H/m denota la permeabilidad magnética del vacío. Supongamos que los datos experimentales han sido recogidos en un archivo CSV:
0.5, 0.1, 0.03, 0.011.0, 0.1, 0.05, 0.011.5, 0.1, 0.07, 0.012.0, 0.1, 0.08, 0.012.5, 0.1, 0.10, 0.013.0, 0.1, 0.11, 0.013.5, 0.1, 0.12, 0.014.0, 0.1, 0.15, 0.01
Para cada línea CSV, la primera entrada corresponde al valor de la corriente eléctrica medida en amperios, mientras que la segunda entrada proporciona su incertidumbre asociada en dicha unidad. De forma similar, la tercera entrada corresponde a la intensidad del campo magnético en el centro de la espira medida en mili-teslas, mientras que la cuarta entrada da cuenta de la incertidumbre asociada expresada en las mismas unidades.
Procederemos, en primer lugar, a incluir las cabeceras estándar a emplear en el programa (para obtener el código completo de este artículo, bastará concatenar los bloques de código siguientes de fondo negro):
#include <concepts>
#include <cstdlib>
#include <fstream>
#include <functional>
#include <sstream>
#include <stdexcept>
#include <string>
#include <tuple>
#include <type_traits>
#include <vector>
Nos serviremos, asimismo, de las siguientes cabeceras de las bibliotecas Matplot++, Range-v3 y mp-units:
#include <matplot/matplot.h>
#include <range/v3/core.hpp>
#include <range/v3/numeric/accumulate.hpp>
#include <range/v3/view/transform.hpp>
#include <units/format.h>
#include <units/math.h>
#include <units/isq/si/electric_current.h>
#include <units/isq/si/magnetic_induction.h>
#include <units/isq/si/permeability.h>
Consideremos una línea CSV almacenada en un objeto std::string. Al igual que hicimos en el segundo artículo de esta serie, definiremos una función variádica parse capaz de parsear dicha línea y retornar, en base a los tipos units::quantity<> que indiquemos como parámetros de la plantilla, una tupla con las cantidades físicas correspondientes:
namespace un = units;
namespace uisq = un::isq;
namespace usi = uisq::si;
template<typename T>
concept Readable = requires (std::istream& is, T& t){ is >> t; };
template<un::Quantity... Qs>
requires (Readable<typename Qs::rep> and ...)
[[nodiscard]] auto parse(std::string const& csv_line, char delim = ',') -> std::tuple<Qs...>
{
auto isstr = std::istringstream{csv_line};
auto set_value = [&](un::Quantity auto& q) -> void {
using Q = std::remove_reference_t<decltype(q)>;
if (auto str_data = std::string{}; std::getline(isstr, str_data, delim)) {
if (auto val = typename Q::rep{}; std::istringstream{str_data} >> val) {
q = Q{val};
}
else throw std::runtime_error{"format error in CSV entry"};
}
else throw std::runtime_error{"missing entries in CSV line"};
};
auto res = std::tuple<Qs...>{};
std::apply([&](auto& ...q){ (..., set_value(q)); }, res);
return res;
}
A continuación, introduciremos una serie de alias convenientes para las magnitudes físicas a emplear como variables independiente (corriente I) y dependiente (campo magnético B), así como para las 4-tuplas (I, ±ΔI, B, ±ΔB):
using x_type = usi::electric_current<usi::ampere>;
using y_type = usi::magnetic_induction<usi::millitesla>;
using tuple_type = std::tuple<x_type, x_type, y_type, y_type>;
Los siguientes functores (véase este post para más detalles) nos permitirán acceder a los datos almacenados en dichas 4-tuplas --así como calcular sus cuadrados-- en base a sus índices de acceso:
template<std::size_t Idx> struct entry {
auto operator()(tuple_type const& t) const { return std::get<Idx>(t); }
};
template<std::size_t Idx> struct entry_sq {
auto operator()(tuple_type const& t) const {
auto const q = std::get<Idx>(t);
return q*q;
}
};
Al proceder a representar gráficamente la nube de puntos experimentales y su recta de mejor ajuste, resultará conveniente poder generar vectores con los valores numéricos correspondientes a las distintas columnas del fichero CSV, prescindiendo de sus unidades de medida. Nuevamente en base al índice de acceso correspondiente, codificaríamos:
template<std::size_t Idx> auto to_num(std::vector<tuple_type> const& data) {
return data
| ranges::views::transform([](auto const& t){ return std::get<Idx>(t).number(); })
| ranges::to<std::vector<double>>;
}
Llegados a este punto, iniciaremos la codificación de la función principal main() estableciendo un flujo de entrada con el fichero CSV con el fin de almacenar sus datos en un vector estándar de 4-tuplas en el que las corrientes, los campos magnéticos y sus incertidumbres asociadas queden registradas con sus correspondientes unidades:
auto main() -> int
try {
auto const data = /* IILE: vector de 4-tuplas (I [A], ΔI [A], B [mT], ΔB [mT]) */ []{
auto csv = std::ifstream{"../../data.csv"};
if (!csv) throw std::ios::failure{"unable to open the CSV file"};
return ranges::getlines(csv)
| ranges::views::transform([](std::string const& ln) -> tuple_type {
return parse<x_type, x_type, y_type, y_type>(ln);
})
| ranges::to<std::vector>;
}();
En base a estos datos, es inmediato calcular la pendiente y la ordenada en el origen de la recta de mejor ajuste para la gráfica B versus I. Obtendremos, asimismo, los errores asociados a dichos valores, así como el coeficiente de correlación de Pearson, según fórmulas bien conocidas para esta clase de regresiones por mínimos cuadrados [3]. Los resultados numéricos coincidirán, por ejemplo, con los proporcionados por la función ESTIMACION.LINEAL de MS Excel [4]:
auto const [slope, slope_err, y_intercept, y_intercept_err, r] = /* IILE */ [&data]{
std::unsigned_integral auto const n = data.size();
auto const x_m = ranges::accumulate(data, x_type{}, ranges::plus{}, entry<0>{}) / n;
auto const y_m = ranges::accumulate(data, y_type{}, ranges::plus{}, entry<2>{}) / n;
auto const sum_x_sq = ranges::accumulate(data, x_type{}*x_type{}, ranges::plus{},
entry_sq<0>{});
auto const sum_y_sq = ranges::accumulate(data, y_type{}*y_type{}, ranges::plus{},
entry_sq<2>{});
auto const sum_xtimesy = ranges::accumulate(data, x_type{}*y_type{}, ranges::plus{},
[](auto&& t){ return std::get<0>(t)*std::get<2>(t); });
auto const xc = sum_x_sq - n*un::pow<2>(x_m);
auto const yc = sum_y_sq - n*un::pow<2>(y_m);
auto const xyc = sum_xtimesy - n*x_m*y_m;
auto const slp = xyc/xc;
auto const u = yc - slp*(sum_xtimesy - n*x_m*y_m);
return std::tuple{
slp, // pendiente
un::sqrt(u/((n-2)*xc)), // error de la pendiente
y_m - slp*x_m, // ordenada en el origen
un::sqrt((u/(n-2))*(1.0/n + un::pow<2>(x_m)/xc)), // error de la ordenada
un::dimensionless<un::one>{xyc/(un::sqrt(xc)*un::sqrt(yc))} // coeficiente R
};
}();
El empleo de la biblioteca mp-units garantiza, en tiempo de compilación, que la totalidad de los cálculos anteriores resulte dimensionalmente correcto. En particular, es inmediato comprobar que la pendiente de la recta y su error asociado (y, equivalentemente, la ordenada en el origen y su correspondiente error) son cantidades de igual tipo:
static_assert(std::same_as<decltype(slope), decltype(slope_err)>);
static_assert(std::same_as<decltype(y_intercept), decltype(y_intercept_err)>);
A continuación, mostraremos en la terminal los valores obtenidos para la pendiente y la ordenada en el origen de la recta de mejor ajuste --acompañados de sus correspondientes errores--, proporcionando el coeficiente de correlación como medida global de la calidad del ajuste:
fmt::print(" slope: ({0:%.3Q} ± {1:%.3Q}) {2:%q}/{3:%q}\n",
slope, slope_err, y_type{}, x_type{});
fmt::print("y-intercept: ({0:%.3Q} ± {1:%.3Q}) {0:%q}\n", y_intercept, y_intercept_err);
fmt::print(" R: {:%.5Q}\n", r);
En el caso de los datos experimentales mostrados al inicio de este artículo, visualizaríamos:
slope: (0.032 ± 0.002) mT/Ay-intercept: (0.018 ± 0.004) mTR: 0.99256
Para R = 60 mm y N = 3, y despreciando el error en la medida del radio de la espira, la permeabilidad magnética del vacío puede estimarse a partir de la pendiente de la recta de mejor ajuste como:
auto const loops = 3;
auto const radius = usi::length<usi::millimetre>{60};
fmt::print("μ_0 = ({0:%.2Q} ± {1:%.2Q}) ⨯ 1.e-6 {0:%q}\n",
1.e+6*un::quantity_cast<usi::henry_per_metre>(2*radius*slope/loops),
1.e+6*un::quantity_cast<usi::henry_per_metre>(2*radius*slope_err/loops));
El valor mostrado en la terminal
μ_0 = (1.27 ± 0.06) ⨯ 1.e-6 H/m
coincide en muy buena aproximación con el esperado, 4π⨯10-7 H/m.
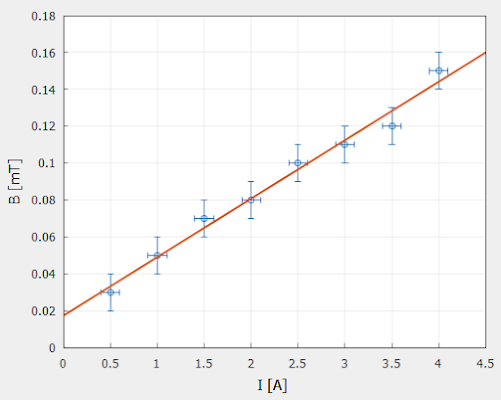
Finalmente, representaremos la nube de puntos experimentales (dotados de barras laterales de error) junto a su recta de mejor ajuste, haciendo uso de la funcionalidad ofrecida por la biblioteca Matplot++:
auto const x = to_num<0>(data);
auto const dx = to_num<1>(data);
auto const y = to_num<2>(data);
auto const dy = to_num<3>(data);
namespace mp = matplot;
mp::errorbar(x, y, dy, dy, dx, dx, "o");
mp::hold(mp::on);
auto ln = [m = slope.number(), n = y_intercept.number()](double x){ return m*x + n; };
mp::fplot(ln)->line_width(2);
mp::hold(mp::off);
mp::axis({0.0, 4.5, 0.0, 0.18});
mp::xlabel(fmt::format("I [{:%q}]", x_type{}));
mp::ylabel(fmt::format("B [{:%q}]", y_type{}));
mp::grid(mp::on);
mp::show();
}
catch (std::exception const& e) {
fmt::print("exception caught: {}\n", e.what());
return EXIT_FAILURE;
}
Referencias bibliográficas
- mp-units - https://mpusz.github.io/units/
- Matplot++ - https://alandefreitas.github.io/matplotplusplus/
- Wikipedia - Regresión lineal - https://es.wikipedia.org/wiki/Regresión_lineal
- MS Excel - Función ESTIMACION.LINEAL - https://support.microsoft.com/es-es/office/funci%C3%B3n-estimacion-lineal-84d7d0d9-6e50-4101-977a-fa7abf772b6d
No hay comentarios:
Publicar un comentario